Welcome to Physics 301! There will be more stuff here soon.
Syllabus and Schedule
You can see the syllabus for the course right here. The table below gives a tentative schedule for the course. These dates are subject to change, depending on the pace of the class.
| Week | Dates | Topics |
|---|---|---|
| 1 | 1/14-1/18 | Intro, Orthogonal coordinate systems |
| 2 | 1/21-1/25 | OCS |
| 3 | 1/28-2/1 | OCS |
| 4 | 2/4-2/8 | Fourier Series |
| 5 | 2/11-2/15 | FS |
| 6 | 2/18-2/22 | FS |
| 7 | 2/25-3/1 | Exam 1, Vector Calc |
| 8 | 3/4-3/8 | Spring Break |
| 9 | 3/11-3/15 | VC |
| 10 | 3/18-3/22 | Series solutions, special functions |
| 11 | 3/25-3/29 | SS, SF |
| 12 | 4/1-4/5 | SS, SF |
| 13 | 4/8-4/12 | Exam 2, Partial differential equations |
| 14 | 4/15-4/19 | PDEs |
| 15 | 4/22-4/26 | PDEs |
Assignments
Assignment 10
Separation of variables, part 2
Due on April 26
Your final homework assignment covers separation of variables in three dimensions (using Cartesian coordinates) and separation of variables in spherical polar coordinates with an axis of symmetry.
Assignment 9
Separation of variables
Due on April 18
Two problems on separation of variables in PDEs with two variables. There is also an optional exercise about solutions of the wave equation in three dimensions (You don't need to hand in the optional problem, but it is instructive to work through!).
Assignment 8
Legendre polynomials, Method of Frobenius
Due on April 5
Exercises involving Legendre polynomials of the first kind, Legendre series representations of functions, and generalized power series solutions of ordinary differential equations using the Method of Frobenius.
Assignment 7
Series Solutions
Due on March 27
This assignment will help you practice working out Maclaurin series solutions of differential equations, and introduce you to series solutions written as expansions around points other than 0.
Assignment 6
Vector Calculus
Due on March 18
A few exercises involving the divergence, curl, and Laplacian in orthogonal coordinate systems; the Divergence Theorem; and Stokes's Theorem.
Assignment 5
Complex Fourier Series, Periods other than 2\(\pi\)
Due on February 22
Now you will determine the complex Fourier Series representations of a few simple functions, and the Fourier Series for periods other than 2\(\pi\). In the last problem you will work out the odd extension of a function from \(0 < x < L \) to \(0 < x < 2L \), and determine the sine series coefficients for the example from our first lecture.
Assignment 4
Basic Fourier Series
Due on February 11
This assignment covers some of the basic (but essential!) integrals needed for evaluating Fourier Series. You will also compute the Fourier Series representation of three simple functions on the interval \(-\pi \leq x \leq \pi\). Be sure to carefully read the statement at the top of assignment!
Assignment 3
Orthogonal Coordinates, Velocity and Acceleration
Due on February 4
In this assignment you will work out the velocity and acceleration vectors in spherical polar coordinates, derive an equation used in our discussion of celestial mechanics, and apply the methods we developed for converting a vector from Cartesian coordinates to another OCS.
Assignment 2
Spherical Polar Coordinates
Due on January 28
In class we learned how to determine the scale factors and basis vectors for any orthogonal coordinate system. For this assignment you will apply this to spherical polar coordinates, which are useful in situations where a system has spherical symmetry.
Assignment 1
Review of Vectors and Multivariable Calculus
Due on January 18
This assignment is a review of some basic material on vectors and multivariable calculus. It's due on Friday of the first week of class. If you have questions you can email or stop by my office!
Working with your classmates on homework is encouraged! But you should only hand in work that you've completed on your own. If your solution looks just like someone else's work then you need to go back and redo it from scratch. If you can't explain each step of your solution then you haven't completed the problem on your own. Remember: the only way to be ready for the exams is to do the homework yourself.
Never, ever hand in an assignment that has been copied from a solutions manual or a source you found online. You won't learn anything that way, and it will earn you a grade of zero for that assignment. If it happens more than once it will be reported to the Department Chair and the Dean. Consider yourself warned. Click here to see the College of Arts and Sciences Statement on Academic Integrity.
References
The main text for the class is Mathematical Methods in Engineering and Physics by Felder & Felder. I've heard great things and expect that it will be very good. The website for the book has lots of supplementary material.
From time to time you may want to consult a different book. If the discussion in Felder & Felder doesn't suit you, or you'd like to see a topic presented differently, or even if you just want to see some additional examples or applications, consider one of the following books:
- Mathematical Methods in the Physical Sciences
Mary L. Boas
- Mathematical Methods for Physics and Engineering
K.F. Riley, M.P. Hobson, and S.J. Bence
- Mathematical Methods for Physicists
George Arfken and Hans Weber
In the past, I taught a different Math Methods course using the book by Boas. Everyone seemed to like it pretty well. The book by Riley et al is more comprehensive, but also kind of terse. Finally, the book by Arfken is a standard text in grad versions of this class. It can be a bit more sophisticated, but maybe you'll like the challenge.
From time to time I may supplement the material from the book with my own notes, which will be posted below.
Notes
A Quantum Mechanical Particle in a Well
Separation of variables is a powerful technique for solving partial differential equations, and you will use it extensively throughout your physics classes. In this example we use S.o.V. to solve an equation similar to one we have already seen in class. Then, we show how this equation arises from the Schrodinger equation for a particles in an infinite potential well, and use what we learned to explain what sorts of energies the particle can have.
A discussion of separation of variables for partial differential equations with two variables. Includes material up through April 18.
Here are a few examples of ODEs solved by assuming a generalized power series.
Series Solutions of ODEs: Examples
Here are three examples of ODEs solved by assuming a Mclaurin series solution. Try to work them out yourselves, then compare what you did with my solutions.
Series Solutions and Special Functions
Many of the ODEs you encounter in physics can be solved by assuming that the solution has a power series expansion. These notes cover the basics of this method, its application to a few equations that frequently appear in physics, and the properties of the resulting “special functions” (like Legendre polynomials and Besssel functions). Current as of 4/2/19.
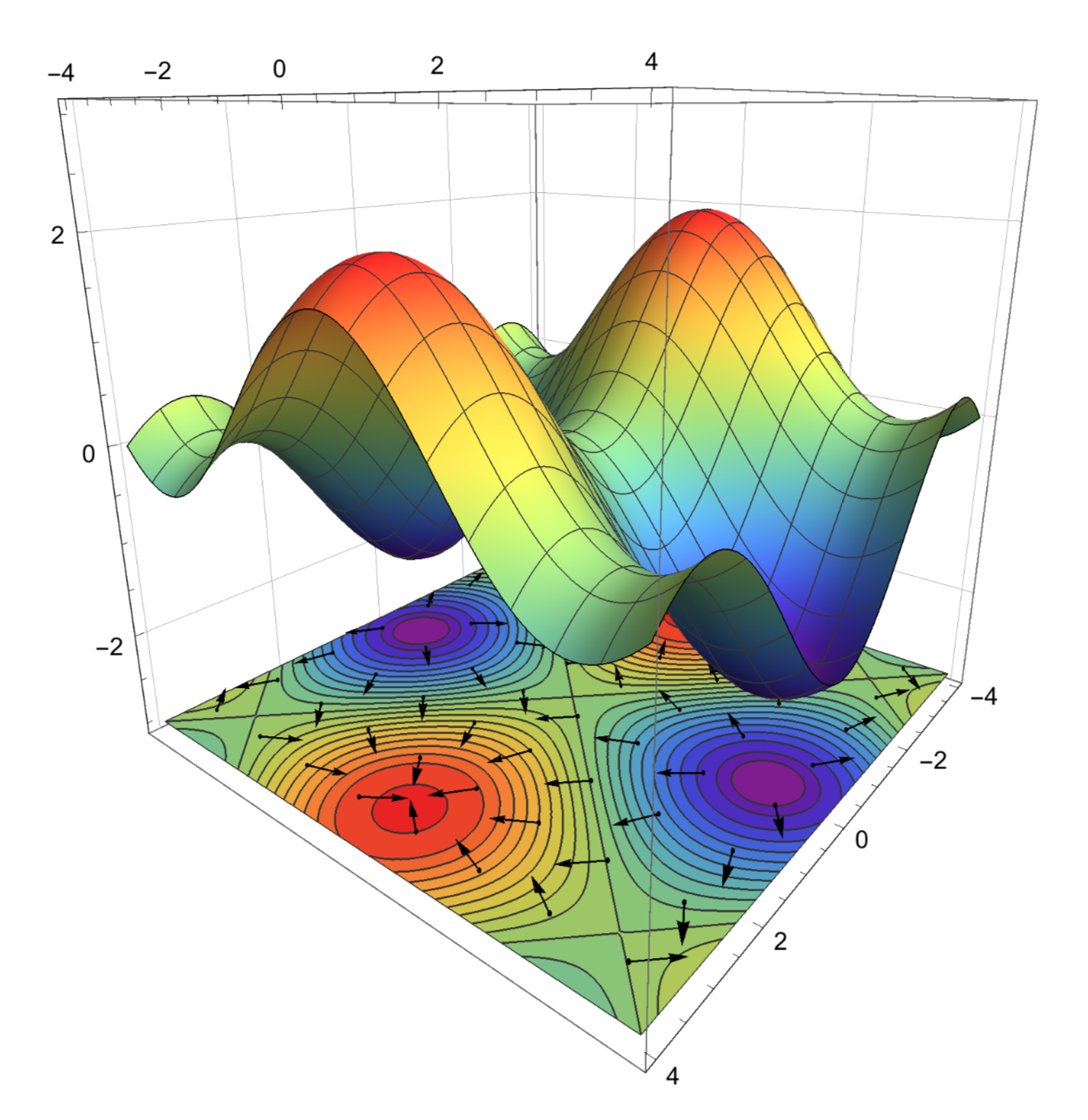
A Mathematica notebook to help us visualize how the gradient of a function is related to the direction in which the function most rapidly increases.
Notes on the gradient, divergence, curl, and Laplacian in general orthogonal coordinate systems, their fundamental theorems, and a brief review of surface and volume integrals.
These notes cover Fourier Series, up to and including our discussion of even and odd extensions on Tuesday, February 19.
A few important facts about Taylor series, Mclaurin series, and what it means to write down an infinite series representation of a function.
Spherical Polar Coordinates and Unit Vectors
As part of homework 2 you derived expressions for \(\hat{r\,}, \hat{\theta\,},\) and \(\hat{\phi\,} \) that you will need to use on homework 3. Since you won't get your graded assignments back before the new assignment is due, I wrote out a short note with the info you need.
Orthogonal Coordinate Systems
Includes material covered through January 29
These notes cover our discussions about Orthogonal Coordinate Systems, up through our discussion of celestial mechanics. The diagrams here are neater than the ones I drew on the board, and there are some extra examples worked out. Also, the text is searchable.
A Brief Introduction to Mathematica
This is just what the title says: A very brief introduction to Mathematica. It shows you a few basics, and should help you take it for a test drive. For a more in-depth introduction I strongly encourage you to work through the first few sections of An Elementary Introduction to the Wolfram Language. Once you're feeling more adventurous, open the “Wolfram Documentation” window from the Help menu and browse some of the topics.
This is a basic review of line integrals -- what they are, how to evaluate them, etc. It may be useful if you're a little rusty on this topic. The file is big (about 22 MB) because of the various plots. Let me know if you find any typos or mistakes and I will post a corrected version.
Stress Relief
If you leave mathematical physics on my chalkboard, my kid will copy it down and yell “I love doing physics.”
